Probability and Linear Difference Equations

Colin Mitchell

Let be the probability that an event occurs on the first in a sequence of trials. We want to find , the probability that it occurs on the nth trial, with the probability that it occurred on the (n - 1)th trial, and with the probability , that it did not occur on the (n - 1)th trial. So we can model this with the linear difference equation

.

So if we rewrite this as

,

we can solve it. If we substitute , we get

.

So a root of this is , which is multiplicity one. So we can form the solution as a combination of the general and particular solutions. Our general solution is of the form

.

The particular solution is

Combining these, we get

.

Since we know , we can find c,

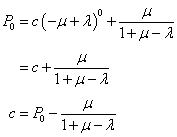
So our final equation becomes