Populations and Harvesting of Fish in a Closed Environment
Colin R. Mitchell
01.24.2008
Introduction
We want to be able to model the populations of fish in a pond as we harvest n fish per year. What we want is to optimize n, so that eventually we do not harvest all of the fish, while harvesting the most fish per year. We can model this by writing the autonomous ordinary differential equation
![]() .
.
From the nature of autonomous ODEs, we know that the if we find the roots of this equation, we can form a phase portrait for the derivative of P. This phase portrait can then be used to identify the behaviour of P with certain starting values. Since ![]() stands for the change in the number of fish per some time t, which we select to represent years, we hope that when we harvest n fish per year, they will grow back by the end of the year, and thus we get that
stands for the change in the number of fish per some time t, which we select to represent years, we hope that when we harvest n fish per year, they will grow back by the end of the year, and thus we get that ![]() , or that the population of fish ultimately does not change in the span of one year.
, or that the population of fish ultimately does not change in the span of one year.
Thus, we can solve for the roots of P, since ![]() is a quadratic, and in doing so we can find the phase portrait, and use that to find the behaviour of the population of our fish pond. So we get
is a quadratic, and in doing so we can find the phase portrait, and use that to find the behaviour of the population of our fish pond. So we get
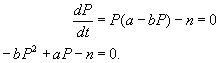
And using the quadratic formula, the roots of P are
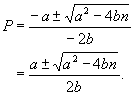
In order for there to be at least one real root for P, we need
![]()
If we get ![]() , however, we get only one root, and this root is semi-stable, and thus our population will not sustain itself. If we get two roots, the larger root is stable, and the smaller root is semi-stable. This implies that if we start with a population of fish that is larger than the smaller root, the population will tend towards the larger root, and thus will be stable when removing n fish per year. So this implies that we need n that satisfies
, however, we get only one root, and this root is semi-stable, and thus our population will not sustain itself. If we get two roots, the larger root is stable, and the smaller root is semi-stable. This implies that if we start with a population of fish that is larger than the smaller root, the population will tend towards the larger root, and thus will be stable when removing n fish per year. So this implies that we need n that satisfies
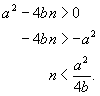
Example
Letís use this equation with some arbitrary figures, so that we can view its behaviour. From our above model, we know that, when ![]() , the maximum population of the fish is
, the maximum population of the fish is ![]() . If we assume that
. If we assume that ![]() ,
, ![]() , we find that the maximum population is
, we find that the maximum population is ![]() fish. Using these values, we then know that we need n to satisfy
fish. Using these values, we then know that we need n to satisfy
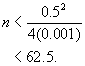
So if we select ![]() , the roots of P are
, the roots of P are
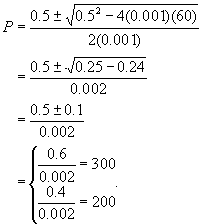
So if we start with a population above 200, the population will tend to go to 300, and thus will be somewhere between 200 and 300 fish.
Conclusion
We can use the above model, and the limit for selecting n, to maximize the number of fish we can harvest per year. If we know how many fish our pond can hold, we can pick a and b, and then find the largest n that will satisfy its limitations. This will give us an idea of what our population will tend towards.