A Second Order Implicit Method for Boundary Condition ODEs

Colin Mitchell

Consider the ODE

We will need to form a system of equations to solve this. First, we need to discretize the left boundary condition, so that we have a starting point. We can do this using a second-order forward difference formula. Using the left boundary condition, we have that

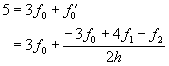
This will be the first line of our matrix. We also need to set up an equation for the right boundary condition. Assuming that we have points in our mesh , when we use a second-order backward difference formula, we get

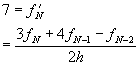
For the rest of the mesh, we can form the general term, centered on ,

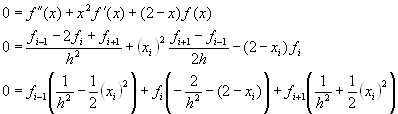
So if we solve the system of equations represented by the matrix

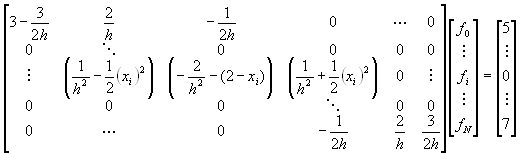
We will have the approximate solution for .